In mathematics, the least common multiple of a group of numbers is the smallest positive number that is divisible by all the numbers. For example, if our numbers are 12 and 15 then the lcm would be 60. It’s also known by other names such as lowest common multiple or smallest common multiple.

For my current project, it’s important that we calculate lcm. That’s another little hint as to what I’m working on😀. To find the lcm there are a few ways, the first I’ll talk about is the manual way. For this, you list all multiples of each number and then find the lowest common number. That’s your lcm

example

12 => 12, 24, 36, 48, 60, 72, 84

15 => 15, 30, 45, 60, 75, 90

In the example above the lowest common number is 60.

There is another way to calculate is to use the gcd.

Greatest Common Divisor

If we have two numbers a and b, then the gcd is the largest number that divides both a and b. For example, for 42 and 56 the gcd is 14.

For calculating gcd we will use the Euclidean algorithm. Here we do an integer division on the larger of the two numbers until one of them is 0. The remaining number will be our gcd.

use std::cmp;

pub fn gcd(a: i64, b: i64) -> i64 {
    if a == b {
        return a;
    }
    let (mut a, mut b) = (a, b);
    loop {
        if cmp::min(a, b) == 0 {
            return cmp::max(a,b);
        }
        (a, b) = if a > b {
            (a % b, b)
        } else {
            (a, b % a)
        };
    }
}
Code language: Rust (rust)

Least Common Multiple

Now we’re back to lcm. The formula is pretty simple.

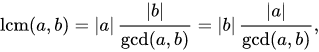
pub fn lcm (a: i64, b: i64) -> i64 {
    a * (b / gcd(a,b))
}
Code language: Rust (rust)

And that’s all she wrote. We now have a function that calculates the lcm for two numbers. We have one more function to create before we get to the actual project and we’ll handle that in the next post.

Until then if you have any questions or comments about today’s problem let me know on Twitter @phoexer and as always happy coding.