Today we have a simple volume problem. Imagine you are stacking cube blocks to make a tower. on the bottom you have n blocks with a total volume of n^3, the next level has n-1 blocks and volume (n-1)^3… until the top with 1 block and a volume of 1^3.

Given a total volume, m, the task is to calculate the value of n if it exists or return -1 if there is no value of n that works.

Thoughts

m is the total volume, i.e. the sum of every layer, and each successive layer is less than the preceding by 1.

So we can think of it as;

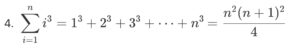
Let’s brute force a tower

We can brute force this pretty easily by just iterating and checking. i.e.

pub fn find_nb(m: u64) -> i32 {
    let mut i:u64 = 1;
    let mut sum: u64 = 0;
    
    loop {
        sum = sum + i.pow(3);
        match sum.cmp(&m) {
            Ordering::Less => {
                i = i + 1;
            },
            Ordering::Equal => return i as i32,
            Ordering::Greater => return -1
        }
    }
}
Code language: Rust (rust)

Looking at the equation image above, you will notice that we have a handy formula. So in theory we can potentially reduce processing time to constant time if we can calculate n based on m.

But I’m not going to do that today, mainly because reasons. Anyway, that’s it for today. Let me know on Twitter how y’all solved this, @phoexer. Happy coding.